John Fenton's Homepage - last updated 31 May 2024

Contact

E-Mail

JohnDFenton@gmail.com

Home address

St-Ulrichs-Platz 2/4
1070 Vienna
Austria

Phones:
Home +43 1 522 7467
Mobile/Handy/Cellulare:
John +43 664 7313 1035
Cristina +43 650 762 2417

Work

Guest Professor
Institute of Hydraulic Engineering and Water Resources Management
TU Wien / Vienna University of Technology
Karlsplatz 13/222, 1040 Vienna, Austria
E-mail: john.fenton@tuwien.ac.at
Homepage: https://www.kw.tuwien.ac.at/en/team/visiting-professors/profile/fenton/

Family History

John's mother spent many years researching the Family History

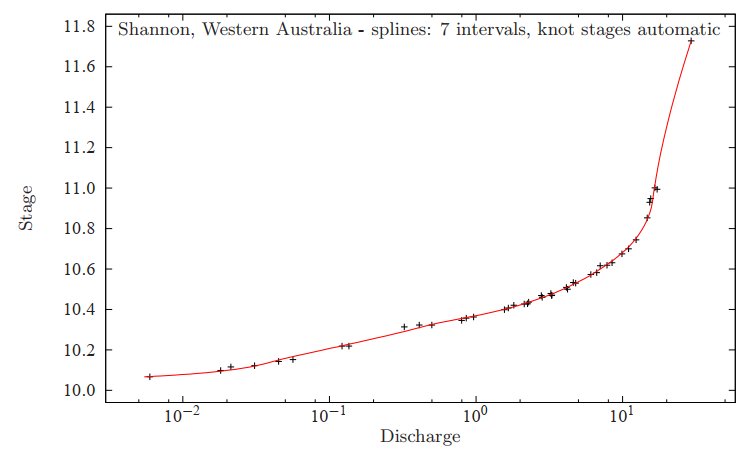
A computer program for calculating rating curves

I have developed a computer program that reads in rating data for a gauging station or structure and calculates a rating curve using least squares methods. It has nothing to do with the old method of trying to fit straight lines on log-log axes. It seems to work well.

The program and its operation are described here.

All files necessary for the operation of the program are in http://johndfenton.com/Rating-curves/Program-Files.exe (it is necessary to copy that link text and paste it into your internet browser). It is a self-extracting file that, when downloaded and executed (after your computer maybe asks you to say that it is acceptable), unpacks the files, retaining the original file structure, under a directory of your choice. The program is based on the research described in two documents:

In those papers a number of different aspects of the problem are considered, including calculating Rating Envelopes for scattered data, and the incorporation of dates of ratings so that one can calculate a rating curve for any day in the past.


A method for approximating, smoothing, differentiating, interpolating, or calculating an envelope to data

While working on river rating curves I developed a program using quadratic or cubic splines. Its primary use was to approximate noisy data, but the method seems quite flexible to approximate more-or-less scattered data, or to smooth, differentiate, interpolate, or calculate an envelope to that data.  An example is Nikuradse's results for resistance in pipes, which shows variable curvature: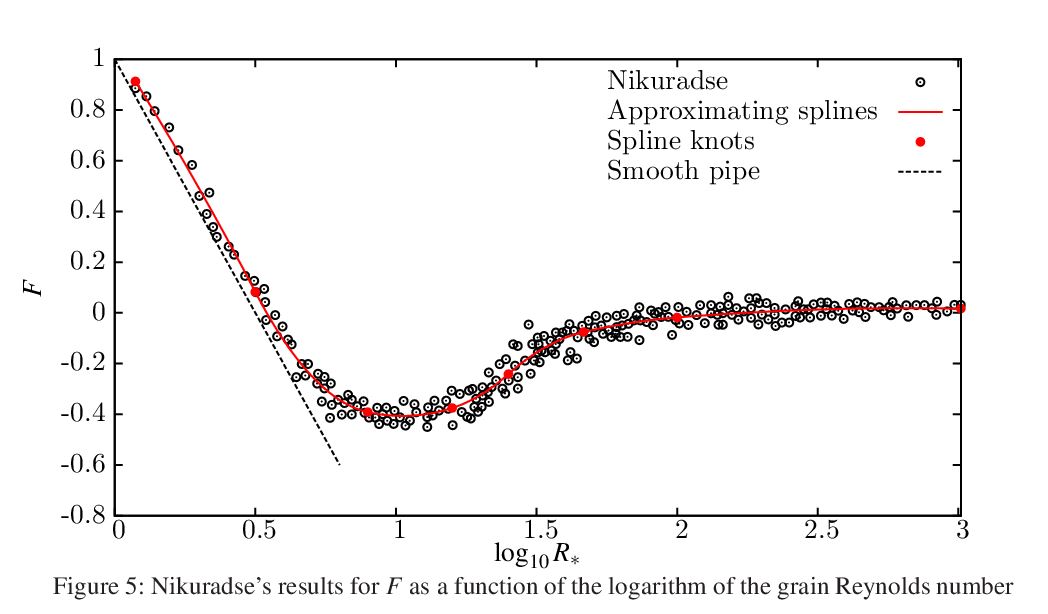


The program and a supporting theoretical document are described here.

 

Collected papers

Full list of papers

Recent publications

  • Fenton, J. D. (2024) The measurement and integration of stream velocity (and almost anything else) using a remarkable formula, Alternative Hydraulics 10
    A proof is given that the traditional two-point formula for integrating velocity measurements in streams is surprisingly accurate, and better than other hydrometric formulae that require more measurements. It is just as accurate for any function or data that are smooth enough to be able to be represented by a polynomial of up to sixth degree
  • Fenton, J. D. (2024) Convolution, deconvolution, the unit hydrograph and flood routing, Journal of Hydrology 634, 131034
    Convolution equations are used to relate the input and the output of a system such as rainfall and runoff, or inflow and outflow of a river reach. There have been numerous reports of unsatisfactory results from the deconvolution necessary to calculate the connecting transfer function. The cause is that the equations are ill-conditioned, and it is shown here that the fundamental theoretical solution is that of wild oscillations such as has often been found computationally. A spectral method is proposed for numerical solution, where, instead of individual point values, the transfer function is expressed as series of given continuous functions, where the problem is to determine the coefficients of those functions. The resulting equations have been found to be well-conditioned, and solutions obtained were smooth, bounded, and enabled a certain amount of physical interpretation of the transfer function. The method has been applied to several problems, including typical rainfall-runoff ones and flood routing and wave propagation problems, with quite satisfactory results. Another problem for deconvolution is found to be the traditional use of truncated equations. A remedy is only to use later output data points where convolution with input data does not reach back beyond the initial one. For the routing of larger flood events, the linear methods employed were found to be not so accurate. However as they are a first approximation that requires no knowledge of stream geometry or resistance, and as either discharge or water level hydrographs can be used, they may be useful.
  • Fenton, John D., Huber, Boris, Klasz, Gerhard and Krouzecky, Norbert (2023) Ship waves in rivers: Environmental criteria and analysis methods for measurements,, River Research and Applications 39(4), 629-647.
    A literature review shows that the most important physical quantities determining environmental impact of ship waves in a waterway are the fluid velocities, maximum and minimum water levels, and size of drawdown events. Fluid velocity can vary strongly in the vertical so that the usual measurements at a single point are not enough unless made near where the effects are most important, often the bed. Customary use of wave height as a measure of impact has been misleading, because the all-important fluid velocity is of a scale given by wave height divided by wave period. A good and simple estimate of the surface velocity as a disturbance scale is shown to be given by the time derivative of the free surface height. The most important role of linear wave theory is to explain and understand the physics and measurement procedures, such as done here in several places. Its use for obtaining numerical results is criticised. Instead, three integral measures of impact are proposed, all of which use surface elevation measurements and which require no essential mathematical approximations or wave-by-wave analysis. The methods are applied to a study of ship waves on the Danube River. A number of results are presented, including examination of the effects of measurement frequency. After a ship passage, due to repeated shoreline reflections of the wake waves, the river is brought into a long-lasting state of short-crested disturbances, with finite fluid velocities. The environmental consequences of this might be important. After the primary and secondary ship waves it could be called the tertiary wave system.
  • Fenton, J. D. (2019) Flood routing methods, Journal of Hydrology 570, 251-264.
    The hierarchy of one-dimensional equations and numerical methods describing the motion of floods and disturbances in streams is studied, critically reviewed, and a number of results obtained. Initially the long wave equations are considered. When presented in terms of discharge and cross-sectional area they enable the development of simple fully-nonlinear advection-diffusion models whose only approximation is that disturbances be very long, easily satisfied in most flood routing problems. Then, making the approximation that changes in surface slope are relatively small such that diffusion terms in the equations are small, various advection-diffusion and Muskingum models are derived. Several well-known Muskingum formulations are tested; one is found to be in error. The three families of the governing equations, the long wave equations, the advection-diffusion and the Muskingum approximations, are linearised and analytical solutions obtained. A dimensionless diffusion-frequency number measures the accuracies of the approximate methods. Criteria for practical use are given, which reveal when they have difficulties for streams of small slope, for fast-rising floods, and/or when shorter period waves are present in an inflow hydrograph. They can probably be used in most flood routing problems with an idealised smooth inflow. However the fact that they cannot be used for all problems requires a general alternative flood routing method, for which it is recommended to use the long wave equations themselves written in terms of discharge and cross-sectional area, when a surprisingly simple physical stream model can be used. An explicit finite difference numerical method is presented that can be used with different inflow specifications and downstream boundary conditions, and is recommended for general use.
  • Fenton, J. D. (2018) On the generation of stream rating curves, Journal of Hydrology 564, 748 - 757.
    Traditional methods for the calculation of rating curves from measurements of water level and discharge are criticised as being limited and complicated to implement, such that manual methods are still often used. Two methods for automatic computation are developed using least-squares approximation, one based on polynomials and the other on piecewise-continuous splines. Computational problems are investigated and procedures recommended to overcome them. Both methods are found to work well and once the parameters for a gauging station have been determined, rating data can be processed automatically. For some streams, ephemeral changes of resistance may be important, evidenced by scattered or loopy data. For such cases, the approximation methods can be used to generate a rating envelope as well, allowing the routine calculation also of maximum and minimum expected flows. Criticism is made of current shift curve practices. Finally, the approximation methods allow the specification of weights for the data points, enabling the filtering of data, especially decreasing the importance of points with age and allowing the computation of a rating curve for any time in the past or present.
  • Fenton, J. D. (2018) Where "Small is Beautiful'' - Mathematical Modelling and Free Surface Flows, Chapter 3 in Free Surface Flows and Transport Processes, Kalinowska, M. B.; Mrokowska, M. M. & Rowiński, P. M. (Eds.), Proc. 36th International School of Hydraulics, Jachranka, Poland, May 2017, Springer.
    Mathematical and computational models in river and canal hydraulics often require data that may not be available, or it might be available and accurate while other information is only roughly known. There is considerable room for the development of approximate models requiring fewer details but giving more insight. Techniques are presented, especially linearisation, which is used in several places. A selection of helpful mathematical methods is presented. The approximation of data is discussed and methods presented, showing that a slightly more sophisticated approach is necessary. Several problems in waves and flows in open channels are then examined. Complicated methods have often been used instead of standard simple numerical ones. The one-dimensional long wave equations are discussed and presented. A formulation in terms of cross-sectional area is shown to have a surprising property, that the equations can be solved with little knowledge of the stream bathymetry. Generalised finite difference methods for long wave equations are presented and used. They have long been incorrectly believed to be unstable, which has stunted development in the field. Past presentations of boundary conditions have been unsatisfactory, and a systematic exposition is given using finite differences. The nature of the long wave equations and their solutions is examined. A simplified but accurate equation for flood routing is presented. However, numerical solution of the long wave equations by explicit finite differences is also simple, and more general. A common problem, the numerical solution of steady flows is then discussed. Traditional methods are criticised and simple standard numerical ones are proposed and demonstrated. A linearised model for the surface profile of a stream is obtained, also to give solutions without requiring detailed bathymetric knowledge.
  

Lectures in hydraulics, numerics, and maritime engineering

River Engineering

The most recent set of lecture notes here are those for a course on River Engineering at the Vienna University of Technology in 2021-2022: Home Page

Lecture notes as slides in colour

Lecture notes for printing in small format, B\&W

A First Course in Hydraulics

This is an introduction to hydraulics. True energy conservation is presented, and Bernoulli's equation is left to a subsidiary (and occasionally useful) role. It is an integrated momentum equation which is valid along a streamline and whose "constant" varies across streamlines. It is absurd to expect to apply it in fully-turbulent three-dimensional situations - for example the flow from a reservoir to a tap in a house. It is much more intellectually honest simply to use conservation of energy, which is more easily derived and is a more plausible model of most hydraulic problems.

Coastal and Ocean Engineering

A final year elective subject, dealing with elementary oceanography, water wave theory, tsunami, and coastal engineering

Computations and Open Channel Hydraulics

An introduction to numerical methods, presenting theory and applications largely using the optimisation package in Microsoft Excel.

Numerical Methods

This is a set of notes describing the application of numerical methods. There are some innovations.

Coastal and Ocean Engineering - Steady water waves

One wave of a steady wave train, showing dimensions, co-ordinates and velocities

A computer program ("Fourier") that solves the problem of steadily-progressing waves over a flat bottom is described and made available here: Fourier

Programs that implement Stokes and cnoidal theories are also available. The instructions file for all is Instructions.pdf., which is also included in Fourier.zip. The latest changes are shown as highlighted comments.

The three wave programs are

  1. A Fourier approximation method whose only approximation lies in truncating the number of terms in the approximating series: Fourier.zip - current version, 23 July 2015.
  2. An implementation of cnoidal theory, which is based on series expansions in shallowness, requiring that the waves be long relative to the water depth : Cnoidal.zip - current version, 20 March 2015 (to be unpacked in a sub-directory of the Fourier one). This is an approximation, and not as applicable to higher waves as the Fourier method. It can be used as a check on that method - for long waves that are not high, both should give the same results.
  3. An implementation of Stokes theory, requiring that the waves be not too long relative to the water depth: Stokes.zip - current version 20 March 2015 (to be unpacked in a sub-directory of the Fourier one). This is also an approximation, and not as applicable to higher waves as the Fourier method. It can be used as a check on that method - for waves that are not high or long, both should give the same results.

Maintained and authorised by John Fenton; Last modified: 31 May 2024