The steadily-progressing wave problem
Solution using programs FOURIER, CNOIDAL and STOKES
The idealisation of a wave
Update Notes - Reverse chronological order
October 2022 - Ibrahim Konuk is writing a C++ program. He
noted that in the C program a couple of variables defined
were not necessary and that for deep water waves a
quantity in the output in a Gnuplot comment line was not
defined. All corrected.
I also modified the Gnuplot files so that the graphical
output mode "qt" is used, rather than "windows". For
screen viewing it is better
July 2019 - For very long waves, say 70 times the water depth, the cnoidal program had problems evaluating the elliptic functions in such an extreme limit. The program has been modified as described in Appendix C-5 of Instructions.pdf, and the software simplified using accurate approximations for all elliptic functions and integrals.
June 2019 - I have modified the program such that Fourier.exe now produces an extra results file Solution-Flat.res, which is rather more easily read automatically - see #7.2 of Instructions.pdf. Of course, all can be accessed by downloading Fourier.zip.
September 2018 - I have just realised that sometime in recent years I had modified the Fourier program to allow for the case of infinite depth, but I had not noted this on the website or in the description file Instructions.pdf.
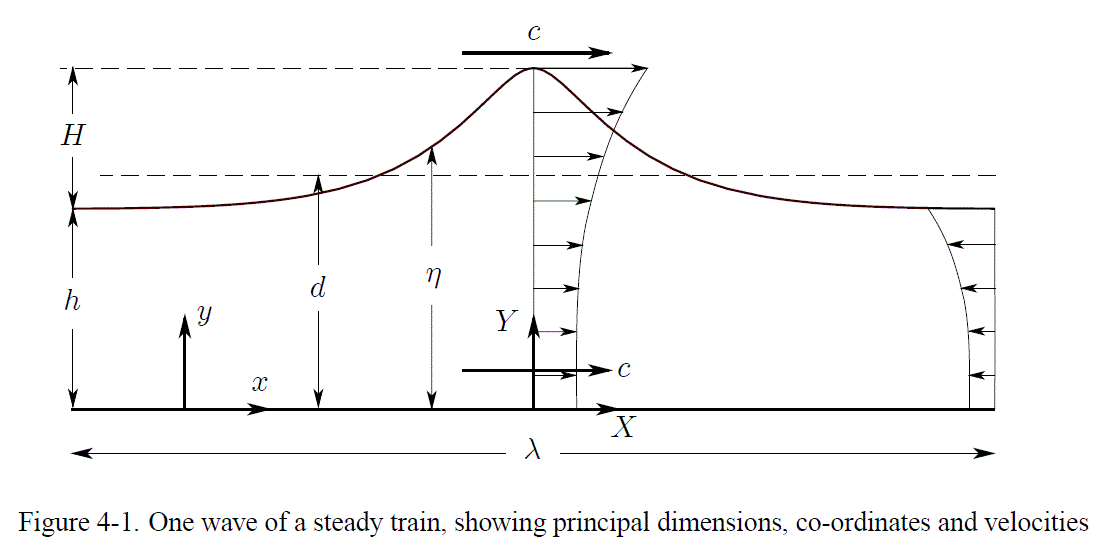
July 2015 - I have added some notes and comments to the file Instructions.pdf. Errors had crept into some of the figures, including the incorrect dimensioning of wave height H on Figure 4-1. The corrected version of the figure is as shown above. I have taken the opportunity to redefine the free surface elevation eta with origin on the bed, as the output from the program uses that. This required changes to the presentation of some of the theory in the document, but is unimportant as far as program operation is concerned. I added a little section on the value of gravitational acceleration g to use. It is more whimsical than anything else, but it does point out that the often-used g = 9.81 m/s^2 is actually not correct to that accuracy for most of the world's population. The changes are described in the comments which are included in that file.
Download programs and instruction manual
There are now threeprograms that can be used. The
instructions file for all is Instructions.pdf,
which is also included in Fourier.zip.
- A Fourier approximation method whose only approximation lies in truncating the number of terms in the approximating series: Fourier.zip - current version, June 2019.
- An implementation of cnoidal theory, which is based on series expansions in shallowness, requiring that the waves be long relative to the water depth : Cnoidal.zip (to be unpacked in a sub-directory of the Fourier one). This is an approximation, and not as applicable to higher waves as the Fourier method. It can be used as a check on that method - for waves that are not high, both should give the same results.
- An implementation of Stokes theory, requiring that the waves be not too long relative to the water depth: Stokes.zip (also to be unpacked in a sub-directory of the Fourier one). This is also an approximation, and not as applicable to higher waves as the Fourier method. It can be used as a check on that method - for waves that are not high, both should give the same results.
Questions, problems: please e-mail me here: John Fenton
Description
The main theories and methods for the steady wave problem which have been used are: Stokes theory, an explicit theory based on an assumption that the waves are not very steep and which is best suited to waves in deeper water; and cnoidal theory, an explicit theory for waves in shallower water. The accuracy of both depends on the waves not being too high. In addition, both have a similar problem, that in the inappropriate limits of shallower water for Stokes theory and deeper water for cnoidal theory, the series become slowly convergent and ultimately do not converge.
An approach which overcomes this is the Fourier
approximation method, which does not use series expansions
based on a small parameter, but obtains the solution
numerically. It could be described as a nonlinear spectral
approach, where a series is assumed, each term of which
satisfies the field equation, and then the coefficients
are found by solving a system of nonlinear equations.
This, originated by Chappelear in 1961, is the basis of
the computer program FOURIER. It has been widely used to
provide solutions in a number of practical and theoretical
applications, providing solutions for engineering and
geophysics. The method provides accurate solutions for
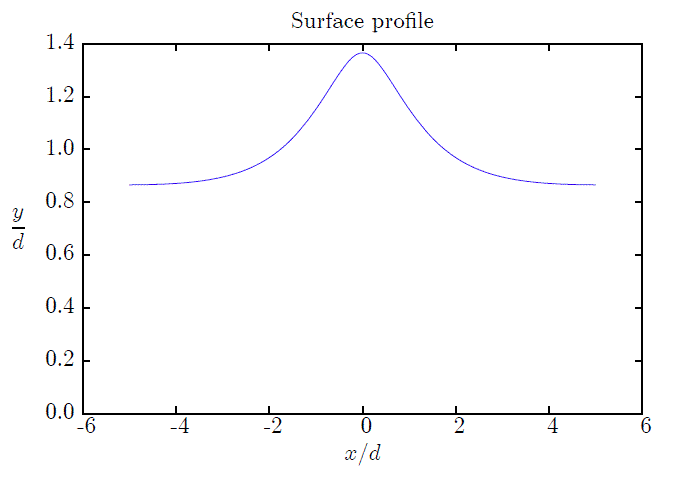
waves up to very close to the highest. Below is shown the
surface profile for a wave of length L/d=50 and a height
98% of the maximum for that length - for such a long and
high wave (approaching a sharp crest), the method is close
to its limits.

The original theory and Fortran code can be found here,
or a more recent presentation here.
The current download version Fourier
also contains the code in the language C++. A description
of the theory and program inputs and outputs is given in Instructions.
A package with programs for cnoidal theory is also
available: Cnoidal.zip, which
is also described in Instructions,
as is a package for Stokes theory: Stokes.zip.
There is also a numerical cnoidal theory where long waves can be treated without difficulty, however for wavelengths at least as long as 50 times the depth, the Fourier method provides good solutions.
Results from Fourier program shown plotted with program Gnuplot
The output from the program is three text files which are
machine readable and can be used for program development
by others. The package also contains plotting files
written in the Gnuplot language (http://www.gnuplot.info/)
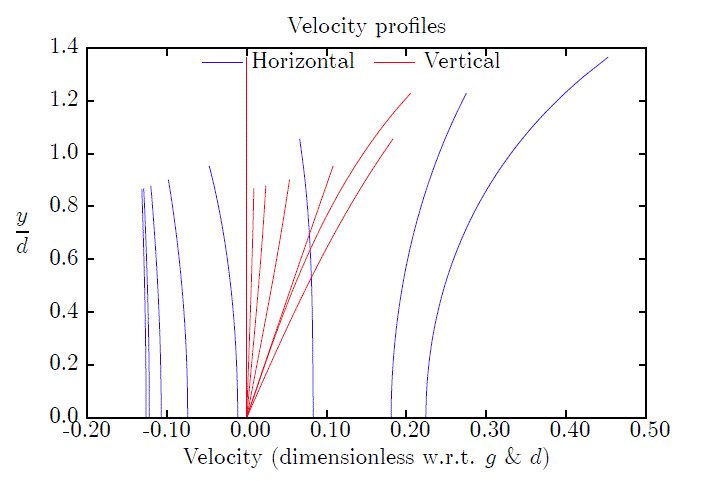
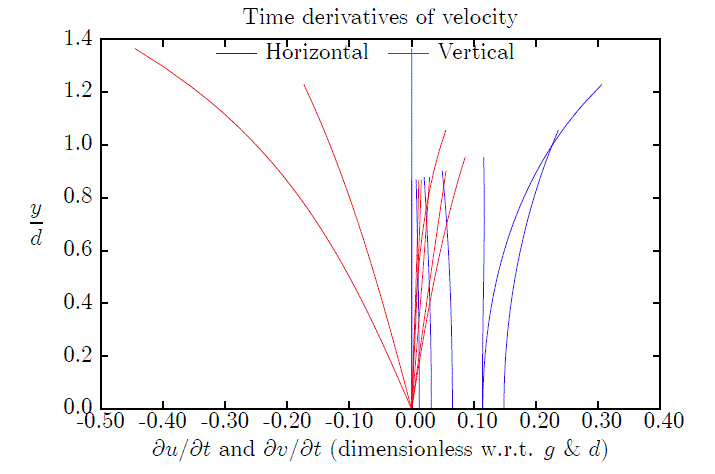
which uses the output to produce figures such as these:
Maintained and authorised by John Fenton;
Last modified: Monday 24 July 2019 Back to Top